Simulated Annealing Algorithm in Lisp
Functions:
(defun linspace (x y n)
(do ((r (list x)
(append (list(+ (car r) (/ (- y x) n))) r)))
((>= (length r) n) (reverse r))))
(defun randnum (&key scale)
(let ((scale1 (if scale scale 1)))
(/
(* scale1 (random 100))
(do ((k (random 100) (random 100)))
((/= k 0) (* scale1 k))))))
(defun randomlize (x &key scale)
(if (atom x)
(float(+ x (- (randnum :scale scale) (randnum :scale scale))))
(map 'list (lambda (xi) (randomlize xi :scale scale)) (coerce x 'list))))
(defun diff (v1 v2)
(if (and (numberp v1) (numberp v2))
(- v1 v2)
(/ (eval(append '(+) (mapcar #'diff (coerce v1 'list) (coerce v2 'list)))) (length v1))))
(defun anneal (f x0 &key min max iter delta scale so)
(if so (format so "temperature x~%"))
(let ((scale1 (if scale scale 1))
(x x0)
(k 1))
(do ((temperature max (* temperature delta)))
((<= temperature min) x)
(if so
(let ((f1 (float(apply f x))))
(if (atom f1)
(format so "~A ~{~A ~} ~A~%" temperature x f1)
(format so "~A ~{~A ~} ~{~A ~}~%" temperature x (coerce f1 'list)))))
(do ((i 1 (+ i 1))
(f1 (apply f x) (apply f x))
(x1 (randomlize x :scale scale1) (randomlize x :scale scale1)))
((> i iter))
(let*((f2 (apply f x1))
(d (diff f2 f1)))
(if (< d 0)
(setf x x1)
(if (/= temperature 0)
(let ((p (exp (/ d (* -1 scale1 temperature)))))
(if (and
(/= p 0)
(< (randnum :scale scale1) p))
(setf x x1))))))))))
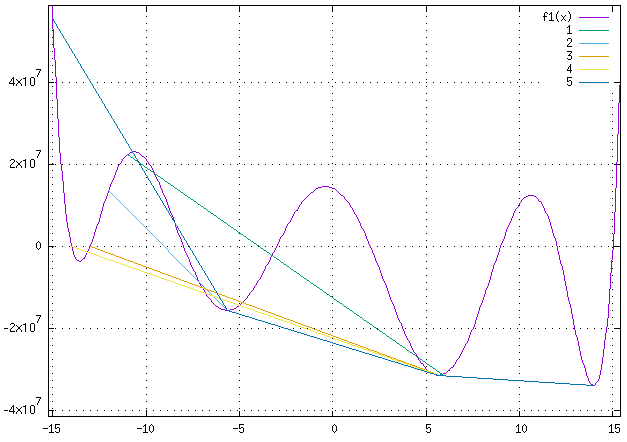
Example:
(defun f1 (x)
(*
(+ x -2)
(+ x 3)
(+ x 8)
(+ x -9)
(+ x -12)
(+ x 13)
(+ x 14)
(+ x -15)
))
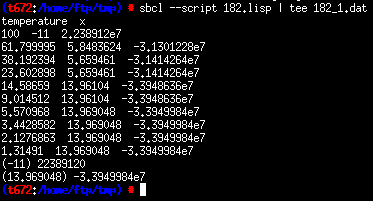
(let*((x1 '(-11))
(x2 (mapcar #'float (anneal 'f1 x1 :min 1 :max 100 :iter 100 :delta 0.618 :so t :scale 1))))
(format t "~A ~A~%" x1 (apply 'f1 x1))
(format t "~A ~A~%" x2 (apply 'f1 x2))
)
Mon Jun 30 15:53:42 JST 2025
Email: Bah4ie@outlook.com

